Curva de Hilbert
Podemos observar que hay un proceso recursivo en la creación de esta curva. Empezamos dividiendo en 4 el cuadrado unitario, de ahí unimos los puntos medios de cada cuadrante en un orden particular este orden nos define una matriz de 2x2, específicamente la matriz \(\begin{pmatrix} 2&3 \\ 1&4 \\ \end{pmatrix}\). Para la siguiente iteración, dividimos el cuadrado unitario en 4 cuadrantes, cada uno de estos cuadrantes tendrá 4 cuadrantes a su vez, donde el cuadrante I tiene como entradas la matriz previamente obtenida, sumándole a cada entrada \(\frac{2*4^{2}}{4}\). El cuadrante II tiene la matriz previamente obtenida sumándole a cada entrada \(\frac{1*4^{2}}{4}\). El cuadrante III tiene la matriz previamente obtenida, pero reflejada por la diagonal perpendicular a la diagonal principal (Denotemos este tipo de transposición como \(\tilde{\tau}\)). El cuadrante IV es la matriz previamente obtenida, pero transpuesta y en cada entrada sumándole \(\frac{3*4^{2}}{4}\).
Esto nos da un claro patrón recursivo, si en el paso \(N\) obtenemos una matriz \(A\), el paso \(N+1\) constará de la siguiente matriz: \(\begin{pmatrix} A+\frac{1*4^{2}}{4}&A+\frac{2*4^{2}}{4} \\ A^{\tilde{\tau}}&A^{\tau}+\frac{3*4^{N}}{4} \\ \end{pmatrix}\)
No olvidemos que cada entrada de la matriz representa el orden en que la curva recorre los cuadrantes para llegar a ese punto, es decir, si un cuadrante tiene el número k, es porque dicho cuadrante es el k-ésimo en ser recorrido.
Podemos calcular \(A^{\tilde{\tau}}\) con el siguiente código:
function trans2(matriz)
k=size(matriz)[1]
new_mat=zeros(size(matriz))
for i=1:k
for j=1:k
new_mat[i,j]=matriz[k+1-j,k+1-i]
end
end
return new_mat
end
trans2 (generic function with 1 method)
Programación de la curva de Hilbert
Empecemos creando el código para calcular la matriz de orden. Este codigo es, como era de esperarse, una función recursiva:
function crear_matriz_orden(num_iteraciones)
long=Int(2^num_iteraciones) #la matriz de orden tendra dimensión (long,long)
matriz=zeros(long,long)
caso_base=[2 3;1 4]
if num_iteraciones==1
return caso_base
else
A = crear_matriz_orden(num_iteraciones-1) #paso recursivo
matriz[1:Int(long/2),1:Int(long/2)]=A.+4^(num_iteraciones-1)#cuadrante arriba izquierda
matriz[1:Int(long/2),Int(long/2)+1:Int(long)]=A.+2*4^(num_iteraciones-1)#cuadrante arriba derecha
matriz[Int(long/2)+1:long,1:Int(long/2)]=trans2(A) #cuadrante abajo izquierda
matriz[Int(long/2)+1:long,Int(long/2)+1:long]=transpose(A).+3*4^(num_iteraciones-1) #cuadrante abajo derecha
end
return matriz
end
crear_matriz_orden (generic function with 1 method)
Una vez que tenemos una matriz de orden, queremos convertir esto a un vector que nos simplifique definir la trayectoria que seguira la curva que vamos a dibujar, para eso es el siguiente código:
function matriz_to_vector_orden(matriz_orden)
k=size(matriz_orden)[1]
p0=[k,1] #Por construcción, el primer punto de la curva de hilbert siempre estará hasta abajo a la izquierda
vector_orden=[] #aquí estará la información de como se recorre la matriz
for i=1:k^2-1
#para cada iteración checaré si el número siguiente está abajo, a la izquierda o arriba, el primer punto será [k,1]
#en cada iteración reasignaré p0 al punto siguiente.
#inicializo variables
tauIz=0
tauDe=0
tauAr=0
tauAb=0
if p0[1]!=k
##checar hacia abajo
tauAb=matriz_orden[(p0+[1,0])[1],(p0+[1,0])[2]]
end
if p0[2]!=1
##checar hacia la izquierda
tauIz=matriz_orden[(p0+[0,-1])[1],(p0+[0,-1])[2]]
end
if p0[2]!=k
##checar hacia la derecha
tauDe=matriz_orden[(p0+[0,1])[1],(p0+[0,1])[2]]
end
if p0[1]!=1
##checar hacia arriba
tauAr=matriz_orden[(p0+[-1,0])[1],(p0+[-1,0])[2]]
end
if tauAb==i+1
p0=p0+[1,0]
push!(vector_orden,"abajo")
elseif tauAr==i+1
p0=p0+[-1,0]
push!(vector_orden,"arriba")
elseif tauIz==i+1
p0=p0+[0,-1]
push!(vector_orden,"izquierda")
elseif tauDe==i+1
p0=p0+[0,1]
push!(vector_orden,"derecha")
end
end
return vector_orden
end
matriz_to_vector_orden (generic function with 1 method)
Por último, definamos las funciones necesarias para crear un dibujo dada una matriz de orden.
function colorear!(matriz, p_i, p_f)
#Dada una matriz y dos puntos colineales de la matriz
p_i=round.(Int,p_i)
p_f=round.(Int,p_f)
if p_i[1]==p_f[1]
#colorear en horizontal
if p_f[2]>p_i[2] #de izquierda a derecha
for i=p_i[2]:p_f[2]
matriz[p_i[1],i]=1
end
elseif p_f[2]<p_i[2] #de derecha a izquierda
for i=p_f[2]:p_i[2]
matriz[p_i[1],i]=1
end
end
elseif p_i[2]==p_f[2]
#colorear en vertical
if p_f[1]>p_i[1] #de abajo hacia arriba
for i=p_i[1]:p_f[1]
matriz[i,p_i[2]]=1
end
elseif p_f[1]<p_i[1] #de arriba hacia abajo
for i=p_f[1]:p_i[1]
matriz[i,p_i[2]]=1
end
end
end
end
function coloreo_dado_orden(iteracion,vec_orden,lenIm=256)
#Los elementos de vec_orden deben ser "arriba","abajo","izquierda","derecha"
#Si la longitud de la imagen es muy pequeña, puede no funcionar el código, también se recomienda que sea potencia de 2
longitud_imagen=lenIm
curva=zeros(longitud_imagen,longitud_imagen)
iter=iteracion
orden=vec_orden
total=4^iter
distancia=1/2^iter
p0=([longitud_imagen,1]+longitud_imagen*[-0.5*distancia,0.5*distancia])
puntos=[p0]
for i in orden
#Para cada iteración, coloreare una distancia hacia la dirección que indica el vector de orden
if i=="arriba"
p0=p0+longitud_imagen*[-distancia,0]
push!(puntos,p0)
elseif i=="derecha"
p0=p0+longitud_imagen*[0,distancia]
push!(puntos,p0)
elseif i=="abajo"
p0=p0+longitud_imagen*[distancia,0]
push!(puntos,p0)
elseif i=="izquierda"
p0=p0+longitud_imagen*[0,-distancia]
push!(puntos,p0)
end
end
for i=1:total-1
colorear!(curva,puntos[i],puntos[i+1])
end
Gray.(curva)
end
coloreo_dado_orden (generic function with 2 methods)
Ensamblemos todas las piezas y pongamos a prueba nuestro código
function CurvaHilbert(iteraciones,tamano=512)#tamaño tiene que ser potencia de 2, y suficientemente grande
coloreo_dado_orden(iteraciones,matriz_to_vector_orden(crear_matriz_orden(iteraciones)),tamano)
end
CurvaHilbert (generic function with 2 methods)
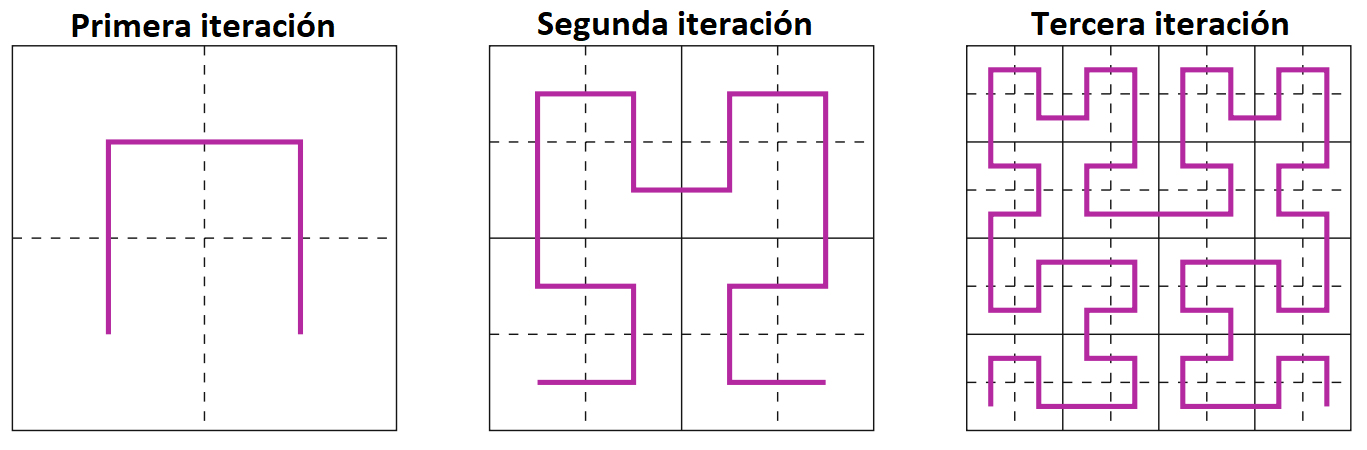
Primera iteración
CurvaHilbert(1,256)

Segunda iteración
CurvaHilbert(2,256)

Tercera iteración
CurvaHilbert(3,256)

Cuarta iteración
CurvaHilbert(4,256)

Quinta iteración
CurvaHilbert(5,256)

Sexta iteración
CurvaHilbert(6,256)

Séptima iteración
CurvaHilbert(7,256)

Conclusiones sobre la curva de Hilbert
De momento hemos visto solo iteraciones de la curva de hilbert, sin embargo, la curva de Hilbert, intuitivamente, es el resultado de llevar este proceso al infinito. Como podemos observar, para cada iteración, la curva se aproxima a llenar el cuadrado. Sin embargo, ¿cómo sabemos que en verdad esta curva es sobreyectiva?
Esto lo podemos deducir del hecho de que cada punto en el cuadrado puede ser aproximado por una sucesión de subcuadrados anidados, y como el espacio es Compacto, esta sucesión converge al único punto que es precisamente el cual define la función de la curva de Hilbert.
Observaciones adicionales
¿Es la curva de hilbert un fractal? Esto dependerá de la definición que se tenga de fractal. En definitiva es en cierto sentido autosimilar pues fue construida de esa forma. Pero si pensamos que la curva es la función, entonces no tiene, de primeras y bajo nuestra base teórica inicial, mucho sentido hablar de funciones fractales. Por otro lado, ¿es la imagen de la función un fractal? Claramente es el atractator de un SFIH, pero, no olvidemos lo que acabamos de demostrar, ¡la imagen de la función es precisamente el cuadrado unitario! cuya dimensión topológica es 2 al igual que su dimensión fractal. Su frontera tiene dimensión topológica 1, lo mismo que su dimensión fractal. Por lo tanto, no cumple ese requerimiento de la definición de fractal.
Algo que es importante de observar es que el código hace mucho énfasis en que la matriz donde se dibuje sea de dimensión \((2^n,2^n)\), por lo que si la dimensión donde se dibuja es distinta, pueden obtenerse curvas parecidas a la de hilbert, pero geométricamente distintas:
CurvaHilbert(7,286)

# Fin